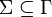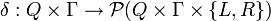La Máquina de Turing (MT) fue introducida por Alan M. Turing en 1936, y puede considerarse como un modelo abstracto que formaliza la idea Intuitiva de algoritmo.

(MT) Es un modelo computacional que realiza una lectura/escritura de manera automática sobre una entrada llamada cinta, generando una salida en esta misma. Este modelo está conformado por un alfabeto de entrada y uno de salida, un símbolo especial llamado blanco (normalmente b, Δ o 0), un conjunto de estados finitos y un conjunto de transiciones entre dichos estados.
Su funcionamiento se basa en una función de transición, que recibe un estado inicial y una cadena de caracteres (la cinta, la cual es finita por la izquierda) pertenecientes al alfabeto de entrada. Luego va leyendo una celda de la cinta , borrando el símbolo , escribir el nuevo símbolo perteneciente al alfabeto de salida y finalmente avanza a la izquierda o a la derecha (solo una celda a la vez), repitiendo esto según se indique en la función de transición, para finalmente detenerse en un estado final o de aceptación, representando así la salida.
Una máquina de Turing con una sola cinta puede ser definida como una 7-tupla ;
 donde:
donde:
 es un conjunto finito de estados.
es un conjunto finito de estados.
 es un conjunto finito de símbolos distinto del espacio en blanco,denominado alfabeto de máquina o de entrada.
es un conjunto finito de símbolos distinto del espacio en blanco,denominado alfabeto de máquina o de entrada.
 es un conjunto finito de símbolos de cinta, denominado alfabeto de cinta.
es un conjunto finito de símbolos de cinta, denominado alfabeto de cinta. 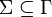
 es el estado inicial.
es el estado inicial.
 es un símbolo denominado blanco, y es el único símbolo que se puede repetir un número infinito de veces.
es un símbolo denominado blanco, y es el único símbolo que se puede repetir un número infinito de veces.
 es el conjunto de estados finales de aceptación.
es el conjunto de estados finales de aceptación.
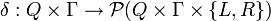
Es una función parcial denominada función de transición,donde  es un movimiento a la izquierda y
es un movimiento a la izquierda y  es el movimiento a la derecha.
es el movimiento a la derecha.
La máquina de Turing puede considerarse como un autómata capaz de reconocer lenguajes formales. En ese sentido es capaz de reconocer los lenguajes recursivamente enumerables, de acuerdo a la jerarquía de Chomsky.
Su potencia es, por tanto, superior a otros tipos de autómatas, como el autómata finito, o el autómata con pila, o igual a otros modelos con la misma potencia computacional. Las maquinas de Turing se pueden representar mediante grafos particulares, también llamados diagramas de estados finitos, de la siguiente manera:
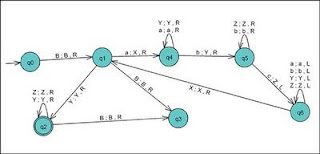
Esta Máquina de Turing está definido sobre el alfabeto Σ={a,b,c}, posee el conjunto de estados
Q={qo,q1,q2,q3,q4,q5,q6}, con las transiciones que se pueden ver. Su estado inicial es q1 y el estado final es q0, el lenguaje de salida δ={X,Y,Z,B} siendo B el símbolo denominado Blanco.
Esta Máquina reconoce la expresión regular de la forma {a^n b^n c^n,n>=0} .
*Los estados se representan como vértices, etiquetados con su nombre en el interior.
*Una transición desde un estado a otro, se representa mediante una arista dirigida que une a estos vértices, y esta rotulada por símbolo que lee el cabezal/símbolo que escribirá el cabezal, movimiento del cabezal .
*El estado inicial se caracteriza por tener una arista que llega a él, proveniente de ningún otro vértice.
*El o los estados finales se representan mediante vértices que están encerrados a su vez por otra circunferencia.
¿COMO FUNCIONA UNA MAQUINA DE TURING?
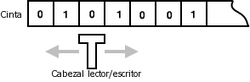
Una máquina de Turing es un dispositivo que transforma un INPUT en un OUTPUT después de algunos pasos. Tanto el INPUT como el OUPUT constan de números en código binario (ceros y unos). En su versión original la máquina de Turing consiste en una cinta infinitamente larga con unos y ceros que pasa a través de una caja.
La caja es tan fina que solo el trozo de cinta que ocupa un bit (0 ó 1) está en su interior. La máquina tiene una serie de estados internos finitos que también se pueden numerar en binario. Para llevar a cabo algún algoritmo , la máquina se inicializa en algún estado interno arbitrario. A continuación , se pone en marcha y la máquina lee el bit que se encuentra en ese momento en su interior y ejecuta alguna operación con ese bit (lo cambia o no, dependiendo de su estado interno). Después se mueve hacia la derecha o hacia la izquierda, y vuelve a procesar el siguiente bit de la misma manera. Al final se para, dejando el resultado al lado izquierdo por ejemplo.
11011i→Una instrucción típica podría ser: 01
VARIANTES DE LA MAQUINA DE TURING
La traducción es como sigue: si la máquina se encuentra en el estado interno 0 y lee 1 en la cinta, entonces pasará al estado interno 1101 (13), escribirá 1 y se moverá hacia la izquierda un paso (la cinta se moverá hacia la derecha). A continuación es conveniente inventar una notación para la secuencia del INPUT. Esta notación se llama notación binaria expandida. Consiste en cambiar la secuencia original binaria por otra construida de la siguiente forma: el 0 se cambia por 0 y el 1 por 10 y se ponen un cero a la izquierda y/o a la derecha del resultado si empieza o acaba en 1 respectivamente. Así por ejemplo, el número 13 que en binario es 1101 es en binario expandido 1010010 con un cero delante por esta última regla 01010010. Para volver al original hay que contraer el binario expandido con la siguiente regla: Empezamos a leer por la izquierda el binario expandido. Cuando encontremos un 0 tomamos nota de cuántos 1 hay hasta llegar al siguiente 0 y lo escribimos. Si encontramos que hay dos 0 seguidos , apuntaríamos un 0 porque no habría ningún 1.Veamos con el 13 cómo se haría.
El primer 0 se encuentra en la primera posición y el siguiente 0 está en la posición 3. Entre los dos solo hay un 1. Lo anotamos. Seguidamente hay un 1, y después un 0, entonces apuntamos 1 porque hay un 1 entre medias de ellos. Esto es lo que se hace sucesivamente y encontramos: 1101 que es el número original.
¿QUE SON Y COMO FUNCIONAN?
Una máquina de Turing consiste, básicamente, en una cinta infinita, dividida en casillas. Sobre esta cinta hay un dispositivo capaz de desplazarse a lo largo de ella a razón de una casilla cada vez. Este dispositivo cuenta con un cabezal capaz de leer un símbolo escrito en la cinta, o de borrar el existente e imprimir uno nuevo en su lugar. Por último, contiene además un registro capaz de almacenar un estado cualquiera, el cual viene definido por un símbolo.
Los símbolos que definen el estado del dispositivo no tienen por que coincidir con los símbolos que se pueden leer o escribir en la cinta. En los programas presentados en el artículo, los posibles símbolos a leer o escribir en la cinta son el 0 y el 1, y los posibles estados se representan con letras mayúsculas. En el emulador , existe un cambio en la representación del estado , usando para ello los números del 0 al 99, para permitir un mayor número de ellos. La máquina tiene un funcionamiento totalmente mecánico y secuencial. Lo que hace es leer el símbolo que hay en la casilla que tiene debajo. Después toma el símbolo del estado en que se encuentra. Con estos dos datos accede a una tabla, en la cual lee el símbolo que debe escribir en la cinta, el nuevo estado al que debe pasar y si debe desplazarse a la casilla izquierda o derecha.
Ejemplo Definimos una máquina de Turing sobre el alfabeto {0,1}, donde 0 representa el símbolo blanco. La máquina comenzará su proceso situada sobre un símbolo “1″ de una serie.
La máquina de Turing copiará el número de símbolos “1″ que encuentre hasta el primer blanco detrás de dicho símbolo blanco. Es decir , situada sobre el 1 situado en el extremo izquierdo, doblará el número de símbolos 1, con un 0 en medio. Así, si tenemos la entrada “111″ devolverá “1110111″, con “1111″ devolverá “111101111″, y sucesivamente.
El conjunto de estados es {s1,s2,s3,s4,s5} y el estado inicial es s1.
La tabla que describe la función de transición es la siguiente:
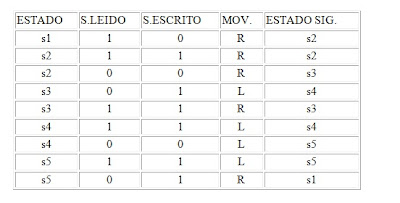
El funcionamiento de una computación de esta máquina se puede mostrar con el siguiente ejemplo (en negrita se resalta la posición de la cabeza lectora/escritora):
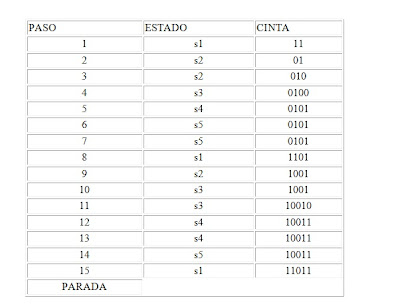
Vemos que esta máquina no hace gran cosa. Sin embargo, una máquina de Turing puede hacer cosas útiles, tales como suma r dos números, multiplicarlos, copiarlos, etc. Disponiendo de una máquina con el suficiente número de estados, podríamos hacer con ella cualquier operación que un ordenador normal pudiese realizar.
Las máquinas de Turing plantean una deducción bastante curiosa: dado que en ellas se puede realizar cualquier trabajo computable , es posible programarlas para que simulen el comportamiento de un potente ordenador. Y como una máquina de Turing puede ser codificada en cualquier ordenador, por pequeño que sea, sería posible (si disponemos de memoria suficiente, claro) emular en nuestro ordenador de casa una máquina de Turing que simule un superordenador. Esto significa que todos los ordenadores pueden realizar exactamente el mismo tipo de tareas , y que los cálculos que pueda realizar el más grande los puede llevar a cabo también el más pequeño. La única diferencia sería, obviamente, la velocidad.
bibliografia:
*Fernando Cuartero
Jose A. Gamez Jose M.
Puerta Departamento de Informatica
* Matemáticas Discretas
Richard Jonhsonbaugh


 es el estado inicial;
es el estado inicial;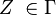 es el símbolo inicial de la pila;
es el símbolo inicial de la pila; es un conjunto de estados de aceptación o finales.
es un conjunto de estados de aceptación o finales. con
con  es la siguiente:
es la siguiente: , es decir no es la palabra vacía, se avanza una posición la cabeza lectora para inspeccionar el siguiente símbolo.
, es decir no es la palabra vacía, se avanza una posición la cabeza lectora para inspeccionar el siguiente símbolo. en la pila del autómata, quedando el símbolo A1 en la cima de la pila.
en la pila del autómata, quedando el símbolo A1 en la cima de la pila.