4.4 Variantes de una maquina de turing

4.- VARIANTES DE UNA MAQUINA DE TURING

Una máquina de Turing puede hacer cualquier cosa que pueda hacer una computadora real y aún cuando una MT no puede resolver ciertos problemas, estos problemas están más allá del los límites teóricos de la computación; es un autómata que se mueve sobre una secuencia lineal de datos. En cada instante la máquina puede leer un solo dato de la secuencia (generalmente un carácter) y realiza ciertas acciones en base a una tabla que tiene en cuenta su "estado" actual (interno) y el último dato leído. Entre las acciones está la posibilidad de escribir nuevos datos en la secuencia; recorrer la secuencia en ambos sentidos y cambiar de "estado" dentro de un conjunto finito de estados posibles. La MT consta de un cabezal lector/escritor y una cinta infinita en la que el cabezal lee el contenido, borra el contenido anterior y escribe un nuevo valor. Las operaciones que se pueden realizar en esta máquina se limitan a:

Avanzar el cabezal lector/escritor para la derecha.

Avanzar el cabezal lector/escritor para la izquierda.

Una máquina de Turing es una tupla de 7 elementos (Q, Σ, Γ, δ, qo, qa(aceptar), qr (rechazar)), donde:

Q, Σ, Γ son conjuntos finitos.

1. Q es el conjunto de estados

2. Σ es el alfabeto de entrada

3. Γ es el alfabeto de la cinta

4. δ: Q x Γ → Q x Γ x { L, R }

5. qo Є Q es el estado inicial

6. qa Є Q es el estado de aceptación

7. qr Є Q es el estado de rechazo, donde qa ≠ qr.

Según va computando una MT, ocurren cambios en el estado actual, el contenido de la cinta y la posición de la cabeza de la cinta. Una combinación de estos tres elementos se llama una configuración de la máquina de Turing. La idea subyacente en el concepto de máquina de Turing es una persona ejecutando un procedimiento efectivo definido formalmente, donde el espacio de memoria de trabajo es ilimitado, pero en un momento determinado sólo una parte finita es accesible. La memoria se divide en espacios de trabajo denominados celdas, donde se pueden escribir y leer símbolos. Inicialmente todas las celdas contienen un símbolo especial denominado “blanco”. La máquina de Turing puede considerarse como un autómata capaz de reconocer lenguajes formales. En ese sentido es capaz de reconocer los lenguajes recursivamente enumérables, de acuerdo a la jerarquía de Chomsky. Su potencia es, por tanto, superior a otros tipos de autómatas, como el autómata finito, o el autómata con pila, o igual a otros modelos con la misma potencia computacional.

Existen muchas alternativas de la máquina de Turing, incluyendo cintas múltiples o indeterminismo. Estas son llamadas variantes del modelo de la máquina de Turing. Tanto el modelo original como sus variantes tienen el mismo poder, es decir, reconocen la misma clase de lenguajes. Para ilustrar la robustez del modelo de la máquina de Turing, hagamos una variación de la función de transición permitida. En la definición original, la función de transición fuerza a la cabeza de la cinta a moverse a la izquierda o a la derecha después de cada paso, la cabeza de la cinta no puede permanecer sin movimiento. Supongamos que le damos a la máquina de Turing la habilidad para que la cabeza de la cinta permanezca sin movimiento. La función de transición tendría la forma δ: Q x Γ → Q x Γ x { L, R, S }.

Los tipos de variantes de una maquina de Turing

Máquina de Turing indeterminista

Una máquina de Turing indeterminista se define de la forma esperada. En cada punto en una computación la máquina puede proceder de acuerdo a varias posibilidades. La función de transición para una máquina de Turing indeterminista tiene la forma

δ: Q x Γ → P(Q x Γ x { L, R })

En general, un cálculo , en una máquina no determinista, es un árbol de descripciones instantáneas (DI), en lugar de ser una secuencia lineal de DI, que es el caso de las máquinas deterministas. En el ejemplo, el árbol de DI es binario. De él representamos solo los dos itinerarios correspondientes a las funciones arriba indicadas:

.... b 1 1 ... 1 b ... s₀

_{/ \}

_{/ \}

s₀ b 1 1 ... 1 b b 1 1 ... 1 b s₂

/ \

-------------- b 1 b 1 ...1 b s₂

-------------- ----------------

s₀ b 1 1 ... 1 b b 1 b ... 1 b s₂

s₀ b 1 1 ... 1 b b 1 b ... b b s₂

s₁ b 1 1 ... 1 1 b

Otros itinerarios corresponden al cálculo de f (x) = 2, 3, etc…

Pero en general, puede ser un árbol cualquiera. Si la máquina está bien construida, para un ejemplar (instance), cada itinerario del árbol conduce a un resultado en general diferente del de los demás itinerarios. Con esta perspectiva uno se puede preguntar si el indeterminismo posibilita el cálculo de funciones que no pueden ser calculadas con máquinas deterministas. La respuesta es NO, porque una función calculable asigna un valor (único) del rango a cada n-upla (entrada) del dominio para la que exista solución. Cada itinerario de una máquina indeterminista corresponde al cálculo de una determinista. En AF y AP es clara la utilidad que tiene construir autómatas finitos no deterministas para facilitar la construcción de los autómatas deterministas correspondientes. Igualmente el concepto es útil en MT.

Cuando la MTND procesa un ejemplar para el que la función está indefinida, se produce un árbol de cálculos que no tiene ninguna hoja con parada por función calculada; es decir, todas las paradas son de función indefinida, o bien no hay parada (cálculo infinito). Pero una máquina no determinista puede ser siempre sustituida por la máquina determinista equivalente con dos paradas, una para función calculada y otra para función indefinida. En la práctica, lo que conviene es detectar las entradas para las cuales la M T no pararía (función parcialmente calculable).

Ejemplo:

Cada máquina de Turing indeterminista tiene una máquina de Turing ordinaria (determinista) equivalente.

1. Si L es reconocido por una MTD, L es reconocido por una Máquina de Turing No Determınista. Las máquinas de Turing deterministas son máquinas de Turing no deterministas en las que solo hay una transición por cada par estado/sımbolo.
2. Si L es reconocido por una MT No Determinista, L es reconocido por una MTD.
Sea MN que acepta L(MN) entonces mostramos que existe M’ que acepta L(M0c=3).
L(MN) = L(M0c=3) y L(M0 : c = 3) = L(M0c=1)
Podemos simular una MTND con una MT determinsta de tres cintas:
1. Se obtiene un n que es el número máximo de transiciones en los conjuntos δ(q, a).
2. En la primera cinta va la cadena de entrada. 3. En la segunda cinta se generan las cadenas sobre el alfabeto 1, 2, ..., n por orden numerico.

Una modificación importante que se puede introducir en nuestra definición original es la eliminación del requerimiento de que la regla de transición sea una función. Esta máquina de Turing se llamára máquina de Turing no determinista, ya que para un estado actual y el símbolo actual de la cinta, puede haber un numero finito de movimientos a elegir. Por tanto, la regla de transición, Δ, de dicha máquina, satisface: Δq, σ⊆ Q ×Γ×{L, R}

Por ejemplo, si la máquina de Turing tiene una transición

Δq, a={(q1, b, R), (q2, a, L)} Entonces los movimientos (q1, abbab) (q1, abbbb) y (q1, abbab) (q2, abbab) Son posibles.

Ya que cualquier máquina de Turing determinista es también no determinista, es lógico que una máquina de Turing determinista se puede simular mediante una no determinista. También una máquina de Turing determinista puede simular una no determinista. Por tanto, no se gana ninguna potencia adicional a causa del no determinismo.

Para ver como se realizaría la simulación, sea M1 una máquina de Turing no determinista que acepta algún lenguaje. Describiremos una máquina de Turing (determinista) M2, que será de tres cintas, que simule M1. Téngase en cuenta que, para cualesquiera estado actual y símbolo de la cinta de M1, hay un número finito de movimientos para realizar a continuación. Numeraremos dichos movimientos 1, 2,…, k. Puesto que tanto Q1 como 1 de M1 son conjuntos finitos, solo existirá un número finito de pares de estado actual y símbolo de la cinta. Por tanto, se puede obtener el par que tenga el mayor número de posibles movimientos a realizar a continuación. Sea este número n. Entonces cualquier computación para M1 se puede representar mediante una secuencia finita de números elegidos entre 1 y n, donde cada número representara el movimiento elegido para ser realizado a continuación en esta etapa de la computación. No toda secuencia finita de número entre 1 y n representan computaciones validas puesto que puede que haya menos de n elecciones para algún par estado-símbolo de la cinta.

En la máquina de Turing de tres cintas, M2, la primera cinta almacenara la entrada y la segunda generará, de forma sistemática, secuencias finitas de números entre 1 y n. Para cada secuencia, M2 copiará la cadena de entrada en la tercera cinta y simulará M1 sobre esta cinta usando la secuencia almacenada en la segunda cinta como guía para realizar la computación. Si una de las secuencias elegidas hace que M1 acepte la cadena, entonces dicha secuencia será generada por M2 y la cadena será aceptada. Si ninguna de las secuencias elegidas provoca la aceptación por parte de M1 entonces tampoco M2 la aceptará. Obsérvese que este razonamiento se redacta en términos de la aceptación de lenguajes. Las máquinas de Turing no deterministas se interpretan como aceptadores de lenguajes. Además se puede generalizar este razonamiento fácilmente, para simular una máquina de Turing multicinta no determinista. En esta sección hemos descrito varias modificaciones a realizar sobre nuestra máquina de Turing original, ninguna de las cuales tiene mayor o menor potencia que la original. Entonces, cabe preguntarse por qué nos hemos molestado en estudiarlas si ninguna de ellas aporta ninguna ganancia en cuanto a capacidad computacional, o por qué no nos hemos centrado en la más sencilla de todas ellas. Una de las razones es que, a partir de ahora, conocemos formas distintas de resolver problemas mediante las máquinas de Turing. Si una de ellas resolviera un problema, de forma más fácil que la original entonces, sin temor a perder generalidad, usaremos dicha variante. Otra razón aun más profunda para el estudio de dichas modificaciones y sus equivalencias con el original, es que con esto se comprende aun más la actualidad de las máquinas de Turing. Cualquier computación que se pueda realizar por medio de una de las nuevas máquinas cae dentro de la categoría de “computable por una máquina de Turing” y, por tanto, es mecánicamente computable.

Maquina de turing con cinta mutipista

Es aquella que mediante la cual cada celda de la cinta de una màquina sencilla se divide en subceldas. Cada subcelda es capaz de contener símbolos de la cinta. La cinta tiene cada celda subdividida en tres subceldas; se dice que esta cinta tiene mutiples pistas puesto que cada celda de esta MT contiene mùltiples caracteres, el contenido de las celdas de la cinta puede ser representado mediante n-tuplas ordenadas. los movimientos que realice esta esta màquina dependeràn de sus estado actual y de la n-tupla que represente el contenido de la celda actual, se podria decir que posee un solo cabezal al igual que una MT sencilla. En el modelo multi-pista, la cinta està dividida en un número finito k de pistas. La funciòn de transicion adquiere la siguiente forma:
δ: Q x Γk → Q x Γk x {D, I, N}
δ(q, (a1, a2, a3, ..., ak)) = (p, (b1, b2, b3, ..., bk), {I,D,N})
Donde los ai y los bi son sìmbolos de Γ.

Las Màquinas de Turing que actùan sobre cinta dividida en k pistas aceptan los mismos lenguajes que las MT estándares.

Es decir el nuevo alfabeto de cinta para k-uplas (s1, s2, ..., sk) es el producto cartesiano Γk=
Γ × Γ... × Γ{kV eces}

Ejemplo: Para representar la suma de dos binarios la MT transformarà:

Máquina de Turing multicinta

Una máquina de Turing multicinta es como una máquina ordinaria con muchas cintas. Cada cinta tiene su propia cabeza de la cinta. Inicialmente la cadena de entrada se encuentra en la cinta 1 y las otras cintas están en blanco. La función de transición se modifica para permitir la lectura, escritura y movimiento de todas las cintas simultáneamente. Formalmente, se define como

δ: Q x Γ k → Q x Γ k x {L, R }k, donde k es el número de cintas. La expresión

δ (qi, a1,…, ak) = (qj, b1, …, bk, L, R, …, L)

Significa que, si la máquina se encuentra en el estado qi y las cabezas 1 a la k están leyendo los símbolos a1 hasta ak, la máquina va al estado qj, escribe los símbolos b1 hasta bk y mueve cada cabeza a la izquierda o derecha según se especifica. Pareciera que las máquinas de Turing multicinta son más poderosas que las máquinas de Turing ordinarias, pero podemos mostrar que son equivalentes. Recordemos que dos máquinas son equivalentes si reconocen el mismo lenguaje.

• Cambia de estado dependiendo del estado actual y del contenido de las celdas de todas las cintas, que estan anlizando actualmente las cabezas de lectura/escritura.


• Escriben un nuevo símbolo en cada una de las celdas barridas por su cabezas de lectura/escritura.


• Mueve cada una de sus cabezas hacia la izquierda o hacia la derecha(de forma independiente al resto de las cabezas).

Tambien son conocidas como máquinas con cintas de varias pistas (MTVP), se le puede ver como máquinas de varias cintas con movimientos sincronizados; MT Y MTVP son equivalentes porque reciprocamente, dada una máquina M^k del tipo MTVP con k pistas, la podemos simular con una máquina M del tipo MT de cualquiera de las dos maneras alternativas:

1. Si A es el alfabeto de M^k, entonces en cada momento el funcionamiento de M^k depende de la lista de k simbolos que aparece en la casilla actual, consistente de K casillas, una por cada pista. Esto define a una máquina de tipo MT sobre el alfabeto A^k que es una potencia cartesiana del original.


2. Consideremos una cinta de una sola pista en donde sus casillas se agrupan en bloques de k casillas. la posición j-èsima de la i-èsima pista en la cinta M^k corresponde a la posición ((j-1)*k+i) -èsima de la nueva cinta. En esta nueva casillas contiguas en la misma pista de M^k distanciaràn de K casillas. El mecanismo de funcionamiento se modifica para que cada movimiento de M^k obligue a revisar un bloque de K casillas y haga la modificaciòn correspondiente, trabajando siempre en bloques.

Por tanto, la función de transición para la máquina de Turing con n cintas es de la forma δ : Q X Гⁿ Q X Гⁿ X { L, P}ⁿ donde una transición de la forma δq, σ1, σ2,…, σn=(p,τ1,τ2, …, τn, (X1, X2,…, Xn)) significa que cambia del estado q a p, reemplaza σi por τi en la cinta i y mueve la cabeza de la cinta i en la dirección Xi.
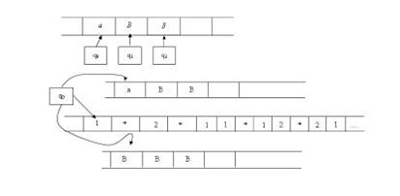
Ejemplo
Construir una MT con dos cintas que acepte el lenguaje L = {aibici i >= 1}
δ(q0, (a,B)) = (q0, (a,X), (D,D))
δ(q0, (b,B)) = (q1, (b,B), (N, I))
δ(q1, (b,X)) = (q1, (b,X), (D, 1))
δ(q1, (c,B)) = (q2, (c,B), (N,D))
δ(q2, (c,X)) = (q2, (c,X), (D,D))
δ(q2(B,B)) = (q3, (B,B), (N,N))

Máquina de Turing Multidimensional

Otra modificación que se puede hacer en nuestra máquina de Turing original es permitir que la cinta tenga muchas dimensiones. Por ejemplo, una cinta de dos dimensiones que se extienda hacia abajo y hacia arriba, al igual que hacia la derecha y hacia la izquierda. Dependiendo del estado actual de la máquina de Turing y del símbolo analizado, cambia de estado, escribe un símbolo en la celda actual y se mueve a la izquierda, a la derecha, hacia arriba o hacia abajo. Por tanto, la función de transición para esta máquina de Turing será de la forma

δ: Q×Γ → Q×Γ×{L,R,U,D}

Una máquina de Turing multidimensional simula, fácilmente, una máquina de Turing estándar. Simplemente realiza todas sus computaciones en una unida dimensión. Una máquina de Turing estándar también puede simular una máquina de Turing multidimensional y, por tanto, la complejidad y flexibilidad adicional que se debe a la múltiple dimensión, no es una capacidad real. Para simular una máquina de Turing de dos dimensiones mediante una máquina de Turing estándar, primero asociaremos una dirección a todas las celdas de la cinta. Una forma de hacerlo es fijar, de forma arbitraria, un lugar en la cinta a partir del cual se asignaran las coordenadas a las celdas de la misma forma que se realiza en el plano de coordenadas. Entonces, se usara una cinta de dos pistas para simular la MT; una pista se encargarà de almacenar el contenido de las celdas y la otra las corrodenadas, utilizando un simbolo (*) para separar los valores de las coordenadas.

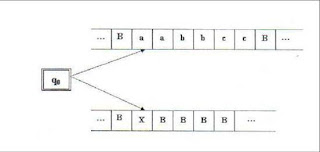
Por ejemplo

Entonces, usaremos una cinta de dos pistas para simular la máquina de Turing. Una pista se encargara de almacenar el contenido de las celdas y la otra las coordenadas. Según esto, si la celda (1,2) contiene una a y la celda (-3, 12) contiene una b, la cinta de la máquina de Turing que realiza la simulación será como

a b

1 * 2 * - 3 * 1 2

Obsérvese que se ha introducido un nuevo símbolo para separar los valores de las coordenadas. Para simular un movimiento de una máquina de Turing de dos dimensiones, esta máquina calcula la dirección de la celda a la que se movería la máquina de Turing de dos dimensiones. Entonces, localiza en la pista inferior la celda con dicha dirección y cambia el contenido de la celda en la pista superior.

Enumeradores

Un enumerador es una máquina de Turing con una impresora, la cual puede utilizarse como un dispositivo de salida para imprimir cadenas.

Un enumerador empieza con una cinta de entrada en blanco. Si el enumerador no se detiene, puede imprimir una lista infinita de cadenas. El lenguaje enumerado por E es la colección de todas las cadenas que eventualmente imprime.

Primero mostraremos que si tenemos un enumerador E que enumera un lenguaje A, una MT M reconoce A. La MT M trabaja de la siguiente manera:

M = “Sobre la cadena de entrada w:

1. Ejecutar E. Cada vez que E imprima una cadena, compararla con w.

2. Si w aparece en la salida de E, aceptar. Claramente, M acepta aquellas cadenas que aparecen en la lista de E.

Ahora demostraremos en la otra dirección. Si la MT M reconoce un lenguaje A, podemos construir el siguiente enumerador E para A. Digamos que s₁, s₂, s₃, … es una lista de todas las posibles cadenas en Σ*.

M = “Ignorar la entrada w:

1. Repetir lo siguiente para i = 1, 2, 3, …

2. Ejecutar M para i pasos sobre cada entrada s₁, s₂, … s_i

3.Si cualquier computación acepta, imprimir la s_k correspondiente Si M acepta una cadena particular s, eventualmente aparecerá en la lista generada por E.

Quíntuple.

En una máquina de Turing con transición quíntuple, la función de transición tiene el siguiente formato:

[ Estado ] [ Símbolo ] → [ Nuevo Estado ] [ Escritura ] [ Desplazamiento ]

Estado = {1, 2,... N } Símbolo = {0, 1} Nuevo Estado = {1, 2,... N} U Estado de parada Escritura = {0, 1} Desplazamiento = {Izquierda, Derecha} (L, R)

Dependiendo del estado actual y el símbolo que haya en la celda actual, la máquina pasa a un estado diferente, escribe un nuevo símbolo y desplaza la cabeza de lectura/escritura a izquierda o derecha.

Cuàdruple

En cuanto a la variante cuádruple, el formato de la función de transición es el siguiente: [ Estado ] [ Símbolo ] → [ Nuevo Estado ] [ Escritura Desplazamiento ]

Estado = {1, 2,... N } Símbolo = {0, 1} Nuevo Estado = {1, 2,... N} U Estado de parada Escritura = {0, 1} Desplazamiento = {Izquierda, Derecha} (L, R)

Es decir, la máquina o escribe un nuevo símbolo en la cinta o desplaza la cabeza de lectura / escritura, pero nunca las dos cosas a la vez.

Este tipo de máquinas tienen algunas restricciones más:

I. Cuando la máquina para solo puede haber una secuencia de 1´s en la cinta.

II. La máquina debe parar con la cabeza de lectura / escritura sobre el 1 situado más a la izquierda de la secuencia.

III. La máquina debería parar después de leer un 1.

La productividad en estas máquinas se define como la longitud de la secuencia de 1´s producida por la máquina de Turing cuando comienza en una cinta en blanco y para al leer el 1 más a la izquierda de la secuencia, dejando el resto de la cinta en blanco. Las máquinas que no paran o que paran en otra situación tienen productividad 0. Cómo apunte cabe destacar que estas máquinas son menos productivas que las quíntuples.

Parada Explícita.

La máquina lee, realiza una acción y a continuación se produce la parada.

Parada implícita.

La máquina lee, y directamente realiza la parada.

.

presentadores:

Pérez Martínez Erika, Francisco Navarro Teresa de Jesús, Montiel Santos Imelda y Mar Gaspar José Eduardo

Referencias:

http://campusvirtual.unex.es/cala/epistemowikia/index.php?title=Castor_Afanoso/Maquinas_Turing

Este link contiene los tipos de variantes de una máquina de Turing pero es un software para interactuar y practicar los autómatas y realizar las transiciones.

http://pisuerga.inf.ubu.es/cgosorio/THOTH/variantes.htm

http://delta.cs.cinvestav.mx/~gmorales/complex/node22.html

http:\\www.laspaginasdelsaber.com\teoriadelacomputationaly\masmamadasmiaslol.htm

http://www.slideshare.net/cchicaiza/mquina-de-turing