Lenguajes Libres de Contexto: Automatas PushDown (Presentan: Ing. Anastasio, Ing. Garcia e Ing. Bautista

AUTÓMATA PUSHDOWN

Este modelo posee dos cintas con celdas iniciales a la izquierda e infinitas celdas a la derecha. Una de sus cintas es para almacenar los símbolos de entrada o palabra a ser analizada y solo se realizan lecturas sobre ella. La otra cinta funciona como una pila ( primer símbolo en entrar, último en salir) sobre ella se introducen y extraen símbolos especiales, a partir de un cabezal de lectura / escritura. Los cabezales están vinculados a una unidad de control.

Inicialmente la cinta de entrada contiene blancos, al igual que la cinta de tipo pila. Se coloca los símbolos que representan la palabra a ser analizada a partir del extremo izquierdo de la cinta de entrada. El cabezal de la cinta de entrada se encuentra, como Estado Inicial sobre el primer símbolo del extremo izquierdo. El cabezal de la cinta de tipo pila se posiciona sobre el tope de la pila o extremo izquierdo de la misma.

Recordemos que el cabezal de lectura de la cinta de entrada solo puede leer un símbolo y desplazarse hacia la derecha. Por otro lado el cabezal de la cinta tipo pila puede escribir un símbolo (generalmente auxiliar) y desplazarse a la derecha o descargar (borrar) un símbolo y desplazarse a la derecha.

Formalmente, un autómata con pila puede ser descrito como una séptupla

M = (S,Σ,Γ,δ, s, Z, F)

donde:

Σ y $Γ$ son alfabetos de entrada, de la cadena y de la pila respectivamente;
S un conjunto de estados;
$\delta: S \times (\Sigma \cup \{\epsilon \} ) \times \Gamma \rightarrow \mathcal{P} ( S \times \Gamma^*)$
$s \in S$ es el estado inicial;
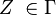$Z\ \in \Gamma$ es el símbolo inicial de la pila;
$F \subseteq S$ es un conjunto de estados de aceptación o finales.

La interpretación de $\delta (s, a, Z) = \{ (s_1, \gamma_1), (s_2, \gamma_2), \ldots, (s_n, \gamma_n) \},$ con $s, p_i \in Q, a \in (\Sigma \cup \{ \epsilon \} ), \gamma_i \in \Gamma$ es la siguiente:

Cuando el estado del autómata es

s

, el símbolo que la cabeza lectora está inspeccionando en ese momento es

a

, y en la cima de la pila nos encontramos el símbolo

Z

, se realizan las siguientes acciones:

Si $a \in \Sigma$ , es decir no es la palabra vacía, se avanza una posición la cabeza lectora para inspeccionar el siguiente símbolo.
Se elimina el símbolo Z de la pila del autómata.
Se selecciona un par $(p i,γ i)$ de entre los existentes en la definición de $δ(s, A, Z)$ , la función de transición del autómata.
Se apila la cadena $\gamma_i = A_1 A_2 \ldots A_k$ en la pila del autómata, quedando el símbolo $A 1$ en la cima de la pila.
Se cambia el control del autómata al estado $p i$ .

Un autómata de pila se encuentra en cada momento en un estado determinado y el estado siguiente depende de los tres elementos siguientes:

• Estado actual

• Símbolo de entrada

• Símbolo superior de la pila

Generalmente, el autómata de pila es no determinista en el sentido de que se permite que haya varias acciones posibles en cada momento.

Un AP puede realizar dos tipos de operaciones elementales:

1. Dependientes de la entrada.

Se lee la cinta y se avanza la cabeza lectora,

En función:

• Del estado actual (qi)

• Del símbolo leído en la cinta (a)

• Del símbolo en la cima de la pila (Z)

Se pasa a un nuevo estado, se elimina el elemento Z de la cima de la pila y se introduce en su lugar una cadena de símbolos.

2. Independientes de la entrada.

Las mismas operaciones que en el caso anterior, sólo que no se lee la cinta, ni se avanza la cabeza lectora. Se maneja la pila sin la información de entrada.

Interpretación de la función de transición

Representaremos con:

(a, b,...) los elementos de Σ

(A, B, C..) los de Γ

(x, y, z,...) los de Σ*

(X, Y, Z,...) los de Γ*

La interpretación de f es:

a) f(q, a, A) = {(q1, Z1), (q2, Z2),... (qn, Zn)}

Cuando el autómata se encuentra en el estado q, lee el símbolo de entrada a y tiene el símbolo A en la cima de la pila; el autómata pasará a algún estado qi (recordar que es no determinista), eliminará el símbolo A de la pila e introducirá en ella la palabra Zi , quedando la cabeza de Zi en la cima de la pila.

b) f(q, λ, A) = {(q1, Z1), (q2, Z2),... (qn, Zn)}

Cuando el autómata se encuentra en el estado q, y tiene el símbolo A en la cima de la pila; el autómata pasará a algún estado qi (recordar que es no determinista), eliminará el símbolo A de la pila e introducirá en ella la palabra Zi , quedando la cabeza de Zi en la cima de la pila.

Se entiende que el resultado de la función f para las configuraciones (estado, símbolo de entrada y símbolo de pila) no explícitamente especificadas es el conjunto vacío. Estas representan configuraciones “muertas” del autómata.

Ejemplo de un Autómata de Pila:

Sea el Siguiente Lenguaje L= { aⁿ(bc^m)^n-1|m³1,n³1 }

TABLA DE TRANSICIONES DEL AUTÓMATA ANTERIOR

Num. Tran.	Estado	Entrada	Símbolo de stack	acciones
1	p	a	S	(p,SAB)
2	p	a	S	(q,b)
3	p	l	S	(p,SAB)
4	q	b	b	(q,l)
5	q	b	B	(q,l)
6	q	c	A	(q,A)
7	q	c	A	(q,l)
8	q	l	B	(r,l)




	Otras combina-ciones				ninguna

A continuación se colocan 3 archivos recopilados de Internet de respetables ingenieros e informáticos:

Link Directo: http://www.dirinfo.unsl.edu.ar/~ayl/Teorias/Apunte_Teoria/Teoria4-07_2.pdf

Link directo: http://www.exa.unicen.edu.ar/catedras/ccomp1/Apunte4.pdf

FUENTES BIBLIOGRÁFICAS:
paginas web...

http://www.ia.urjc.es/grupo/docencia/automatas_itis/apuntes/capitulo11.pdf
http://es.wikipedia.org/wiki/Aut%C3%B3mata_con_pila

LIBROS COMO...
1.-TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES. AUTÓMATAS Y COMPLEJIDAD
KELLY DEAN

EDITORIAL PRENTICE HALL

PRESENTARON:

Leen Christian Anastasio Hernández .

Marissey Bautista Alonso.

Jorge Eduardo García Morales.

Lenguajes Libres de Contexto

miércoles, 30 de marzo de 2011

Automatas PushDown (Presentan: Ing. Anastasio, Ing. Garcia e Ing. Bautista

No hay comentarios:

Publicar un comentario